Secondary Mathematics
Secondary Math Program Goals
-
Goal 1: The district will support the adoption of resources, writing of curriculum, creation of assessments, and provide content-specific professional learning to support teacher implementation and meet individual student needs.
Goal 2: Teachers will implement district adopted curriculum, resources, and assessments with integrity.
Goal 3: Students will engage in rigorous grade-level math learning opportunities that include best practices for equitable instruction and sense making.
Goal 4: Through participation in secondary mathematics courses, students will have the skills necessary to continue rigorous coursework in high school, as well as be equipped to enter higher education institutions or careers of their choice.
Core & Adaptive Software Resources
-
Core Resources Adaptive Software 

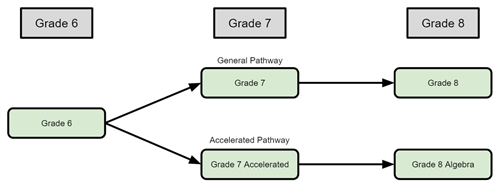
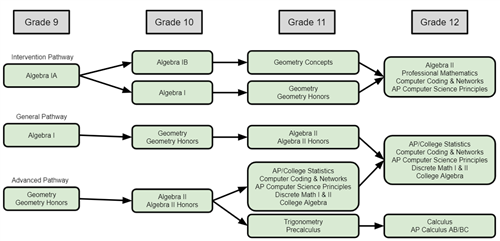
SPS Mathematics Pathways
-
At this time, teacher recommendation is necessary for students to be enrolled in the Accelerated/Advanced/Intervention Pathway.
Best Practice
-
Core Beliefs About Mathematics in SPS
- In mathematics, learning should focus on developing an understanding of grade-level concepts and procedures through problem solving, reasoning, and discourse.
- In mathematics, students need to have a range of strategies and approaches from which to choose in solving problems, including, but not limited to, general methods, standard algorithms, and procedures.
- In mathematics, students can learn through exploring and solving contextual and mathematical problems.
- In mathematics, the teacher will engage students in tasks that promote reasoning and problem solving and facilitate discourse that move students toward shared understanding of mathematics.
- In mathematics, the student will be actively involved in making sense of mathematics tasks by using varied strategies and representations, justifying solutions, making connections to prior knowledge and familiar contexts and experiences, and considering the reasoning of others.
- In mathematics, students are provided with appropriate challenges, encouraged to persevere in solving problems, and supported in productive struggle in learning.
- In mathematics, students have:
- The right to be confused
- The right to claim a mistake
- The right to speak, listen, and be heard
- The right to write, do, and represent what makes sense
-
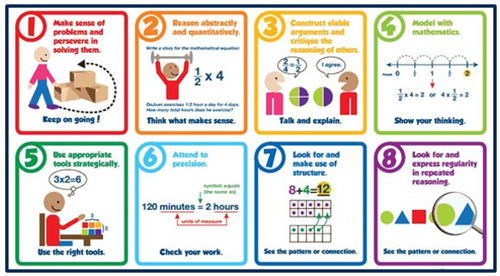
Standards for Student Mathematical Practice
The Standards for Mathematical Practice describe varieties of expertise that mathematics educators at all levels should seek to develop in their students.
-
Effective Mathematics Teaching Practices
The teaching of mathematics is complex. It requires teachers to have a deep understanding of the mathematical content that they are expected to teach and a clear view of how student learning of that mathematics develops and progresses across grades. It also calls for teachers to be skilled at using instructional practices that are effective in developing mathematics learning for all students. The eight Mathematics Teaching Practices illustrated below describe the essential teaching skills derived from the research-based learning principles, as well as other knowledge of mathematics teaching that has emerged over the last two decades.
-
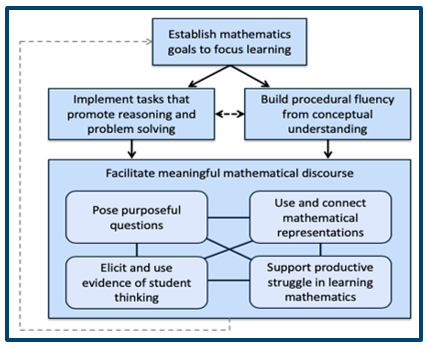
Orchestrating Productive Mathematics Discourse
Research shows there are best practices that can be used to create a classroom environment that fosters rich classroom discussions. The below visual describe five specific practices teachers can use to plan and lead productive math discussions. The five practices are viewed as critical components of a well-designed plan to make purposeful and thoughtful decisions that ultimately strengthen students’ understanding of robust mathematics.
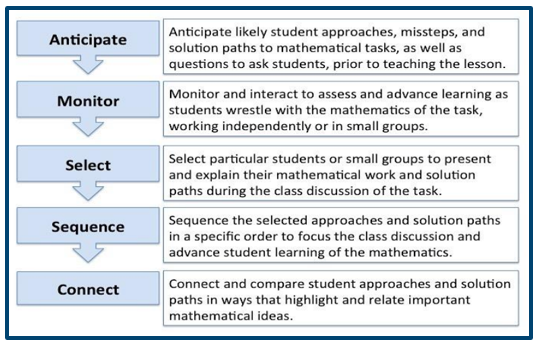
-
A Problem-Based Model
In order to learn mathematics, students should spend time in math class doing mathematics.
Students learn mathematics as a result of solving problems. Mathematical ideas are the outcomes of the problem-solving experience rather than the elements that must be taught before problem solving.
Students should take an active role, both individually and in groups, to see what they can figure out before having things explained to them or being told what to do. Teachers play a critical role in mediating student learning, but that role looks different than simply showing, telling, and correcting. The teacher’s role is:

Teachers should build on what students know. New mathematical ideas are built on what students already know about mathematics and the world, and as they learn new ideas, students need to make connections between them. In order to do this, teachers need to understand what knowledge students bring to the classroom and monitor what they do and do not understand as they are learning.
Each and every student should have access to the mathematical work. With proper structures, accommodations, and supports, all students can learn mathematics. Teachers’ instructional toolboxes should include knowledge of and skill in implementing supports for different learners.
- KAC
| Showing results for "Professor named Smith at Elementary School" |
- Whitney Evans


